Abbiamo spesso parlato di un metodo alternativo di propulsione spaziale a vele solari. Il concetto è spiegato proprio dal suo nome: per muoversi il veicolo spaziale dispiega una vela per utilizzare la pressione della luce solare per creare spinta, in modo simile a come le barche a vela convenzionali usano la pressione del vento.
Diversi lettori hanno fatto domande su queste vele solari e il problema principale che solleva interrogativi è come i fotoni possano esercitare pressione sulla vela quando non hanno massa. Cerchiamo di capirlo.
Johannes Kepler nel XVII secolo suggerì per primo l’idea che la luce potesse esercitare una pressione. Venne ispirato dalla deflessione delle code delle comete che passano vicino al Sole. Nel XIX secolo, James Clerk Maxwell fornì una spiegazione teorica per la pressione della luce. Successivamente, la pressione della luce è stata studiata attraverso esperimenti dal fisico russo Pyotr Lebedev.
I venti che spingono le barche a vela convenzionali trasmettono slancio alla vela. Ma se cerchiamo la definizione di quantità di moto, notiamo facilmente che la quantità di moto è il prodotto di massa e velocità. Quindi, come può la luce trasferire quantità di moto se non ha massa?
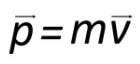
Nella fisica newtoniana, la pressione della luce su vele solari è impossibile. La buona notizia è che la fisica newtoniana ha un campo di applicabilità limitato; pertanto, le vele solari funzionano. A proposito, nel 2010, la navicella spaziale IKAROS ha raggiunto Venere utilizzando una vela solare. La risposta alla domanda su come la luce possa trasferire la quantità di moto si trova nella teoria della relatività ristretta.
Nella teoria della relatività, le quantità fisiche, come la quantità di moto, la velocità, ecc., sono rappresentate come quattro vettori nello spazio quadridimensionale di Minkowski. Sono chiamati quattro momenti, quattro velocità, ecc. L’uso di questi vettori è estremamente conveniente per i calcoli relativistici perché sono invarianti rispetto alla transizione da un sistema di riferimento a un altro (vedi covarianza di Lorentz).
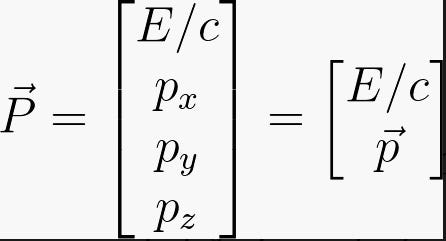
Il modo in cui il quadrimomento cambia durante le trasformazioni di Lorentz, quando si passa da un sistema di riferimento a un altro, dimostra che il momento è inseparabilmente legato all’energia.
Analogamente a come lo spazio e il tempo sono considerati un’unica entità, lo “spaziotempo”, anche l’energia e la quantità di moto sono unificate.
Di conseguenza, diversi osservatori possono interpretare l’energia e la quantità di moto di un oggetto in modo diverso. Ciò che un osservatore percepisce come energia, un altro può percepirlo sia come energia che come quantità di moto e viceversa. Indipendentemente dal sistema di riferimento dell’osservatore, la relazione tra quantità di moto ed energia è determinata dalla seguente equazione:
Se sostituiamo la massa di un fotone, che è zero, nell’equazione di cui sopra, risulta che un fotone ha ancora quantità di moto, che può essere espressa come:
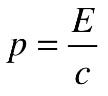
Pertanto, entrando in collisione con le vele, un fotone, secondo la legge di conservazione della quantità di moto, trasferisce la sua quantità di moto alle vele, esercitando una pressione.
Quanta luce è necessaria per accelerare un veicolo spaziale?
Un singolo fotone ha una piccolissima quantità di moto. L’energia di un fotone dipende dalla frequenza della luce. È facile calcolare che, ad esempio, un singolo fotone in un raggio di luce monocromatica con una frequenza di 5*10 ¹⁴ hertz crea una quantità di moto di circa 1,11 * 10⁻²⁷ kg m/s. Fortunatamente, il Sole emette un numero enorme di fotoni. Quindi, per effettuare una spinta di 10 newton sulla superficie della vela, circa 9 * 10²⁷ fotoni spontanei al secondo dovrebbero colpire la vela.
Questo significa, quindi, che per muovere una navicella spaziale occorreranno vele molto grandi, le cui dimensioni potranno essere calcolate matematicamente partendo dalla massa dela navicella ed utilizzando le relazioni indicate sopra.
