Ecco una domanda che alla maggior parte di noi è stata posta ad un certo punto della nostra vita, “qual è la distanza più breve tra due punti?”
Per impostazione predefinita, la maggior parte di noi darà la stessa risposta che Archimede ha dato più di 2.000 anni fa: una linea retta.
Se prendi un foglio di carta piatto e metti su di esso due punti in qualsiasi posizione, puoi collegare quei due punti con qualsiasi linea, curva o percorso geometrico che puoi immaginare. Finché la carta rimane piatta, non curva e non piegata in alcun modo, la linea retta che collega questi due punti sarà il modo più breve per collegarli.
Questo è esattamente il modo in cui funzionano le tre dimensioni dello spazio nel nostro universo: nello spazio piatto, la distanza più breve tra due punti qualsiasi è una linea retta. Ciò è vero indipendentemente da come ruoti, orienti o posizioni in altro modo quei due punti.
Ma il nostro Universo non è costituito semplicemente da tre dimensioni spaziali, ma da quattro dimensioni spazio-temporali. È facile guardarlo e dire: “Oh, beh, tre di loro sono lo spazio e uno di loro è il tempo, ed è lì che otteniamo lo spaziotempo“, e questo è vero, ma non l’intera storia.
Dopo tutto, la distanza più breve tra due eventi spaziotemporali non è più una linea retta. Ecco la scienza del perché.
Annuncio pubblicitario
Interessato all'Intelligenza Artificiale?
Prova a leggere su Amazon Unlimited la nostra guida su come installarne una in locale e come ricavarne il massimo.
Una Intelligenza Artificiale locale ti permette di usufruire di tutti i vantaggi derivanti dall'uso dell'IA ma senza dover pagare costosi abbonamenti.
📘 Leggi la guida su AmazonPer la maggior parte di noi, la nostra prima esposizione all’idea che una linea retta sia la distanza più breve tra due punti proviene da un concetto che potremmo non realizzare: il teorema di Pitagora.
Potresti ricordare il teorema di Pitagora come regola sui triangoli rettangoli, secondo cui i quadrati costruiti sui lati corti (o cateti) sommati insieme, sono uguali al quadrato costruito sul lato lungo (o ipotenusa).
In termini matematici, se i lati corti sono a e b mentre il lato lungo è c , allora l’equazione relativa è a² + b² = c² .
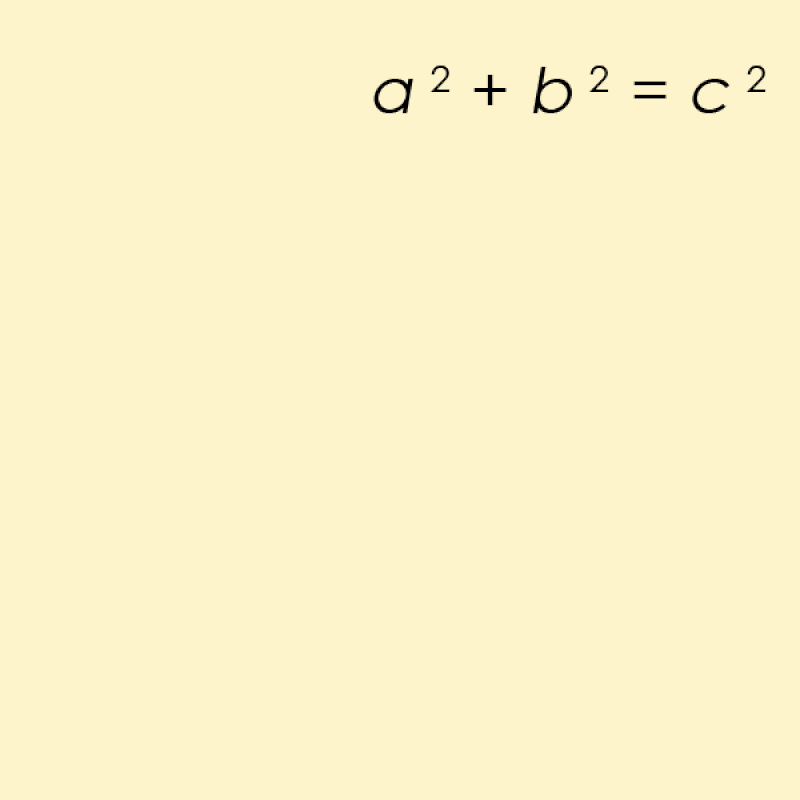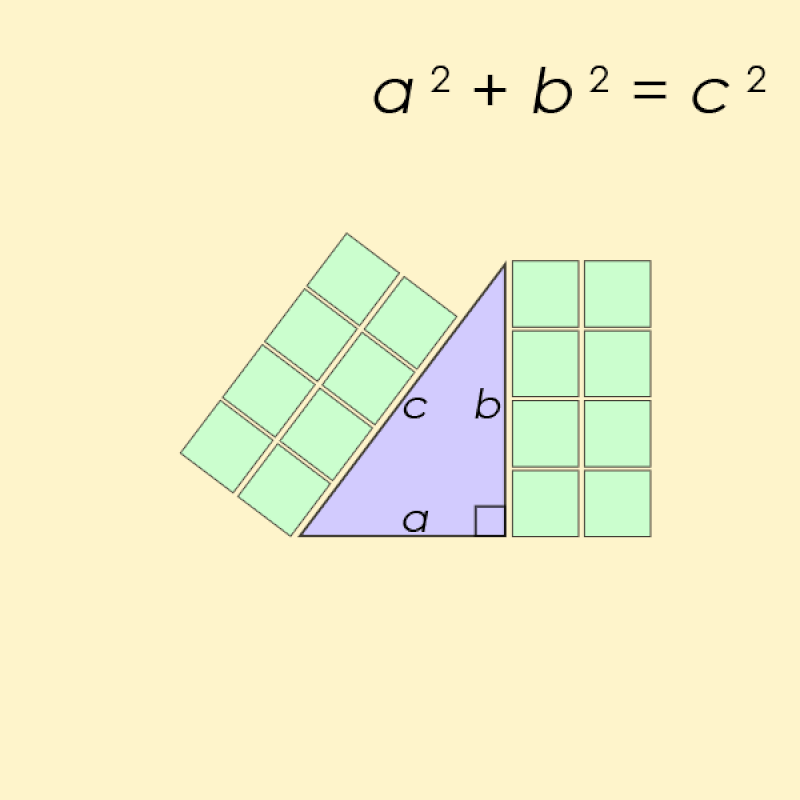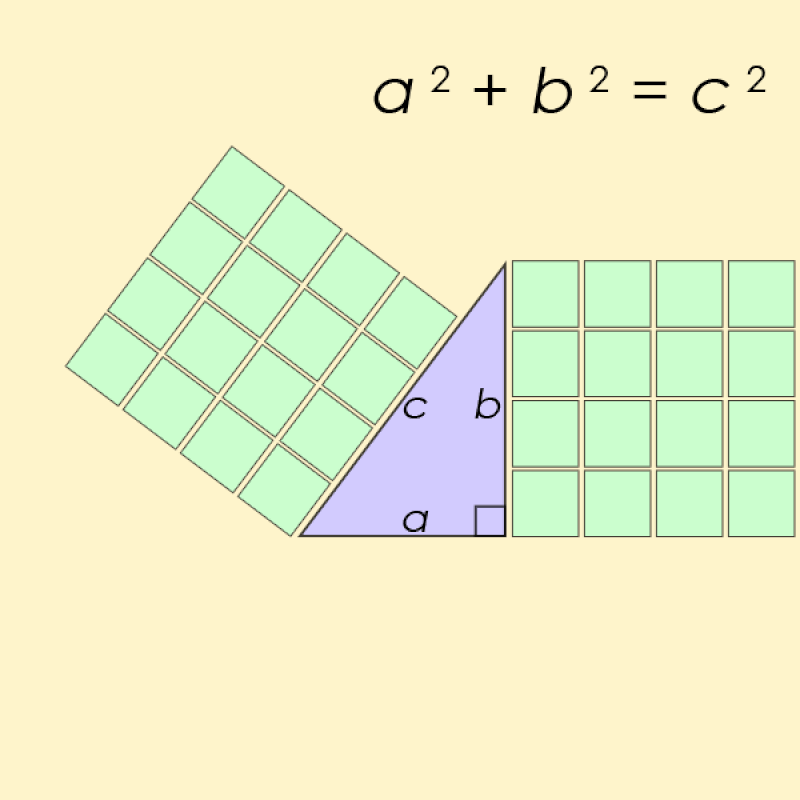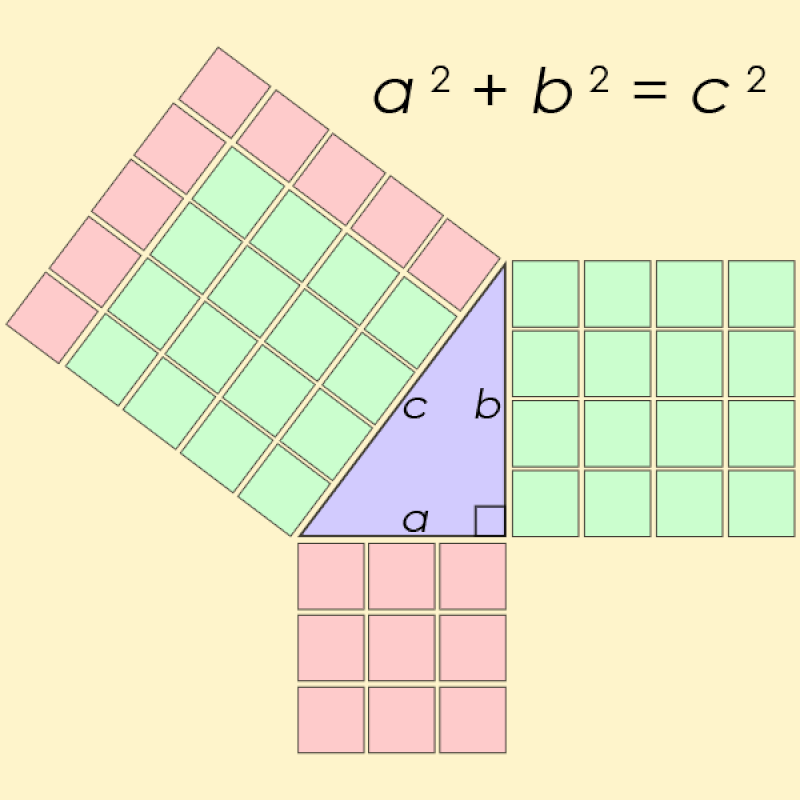
Nel nostro universo, ovviamente, non viviamo su un foglio di carta piatto. Abbiamo non solo la lunghezza e la larghezza come dimensioni al nostro universo, ma anche la profondità.
Se vuoi capire qual è la distanza tra due punti qualsiasi nello spazio, devi usare esattamente lo stesso metodo che usavi in due dimensioni, tranne che devi inserire una dimensione extra. Qualunque sia la quantità di separazione dei due punti nella direzione x , la direzione y e la direzione z , puoi calcolare la distanza totale tra di loro esattamente come prima.
Solo che, a causa della dimensione extra, la distanza tra loro – chiamiamola d – sarà data da d = √ ( x ² + y ² + z ²). Potrebbe sembrare un’equazione complicata, ma dice solo che la distanza tra due punti qualsiasi è definita dalla linea retta che li collega: la linea che rappresenta la separazione tra i due punti in tutte e tre le dimensioni: la direzione x , la y -direction e z -direction combinati.
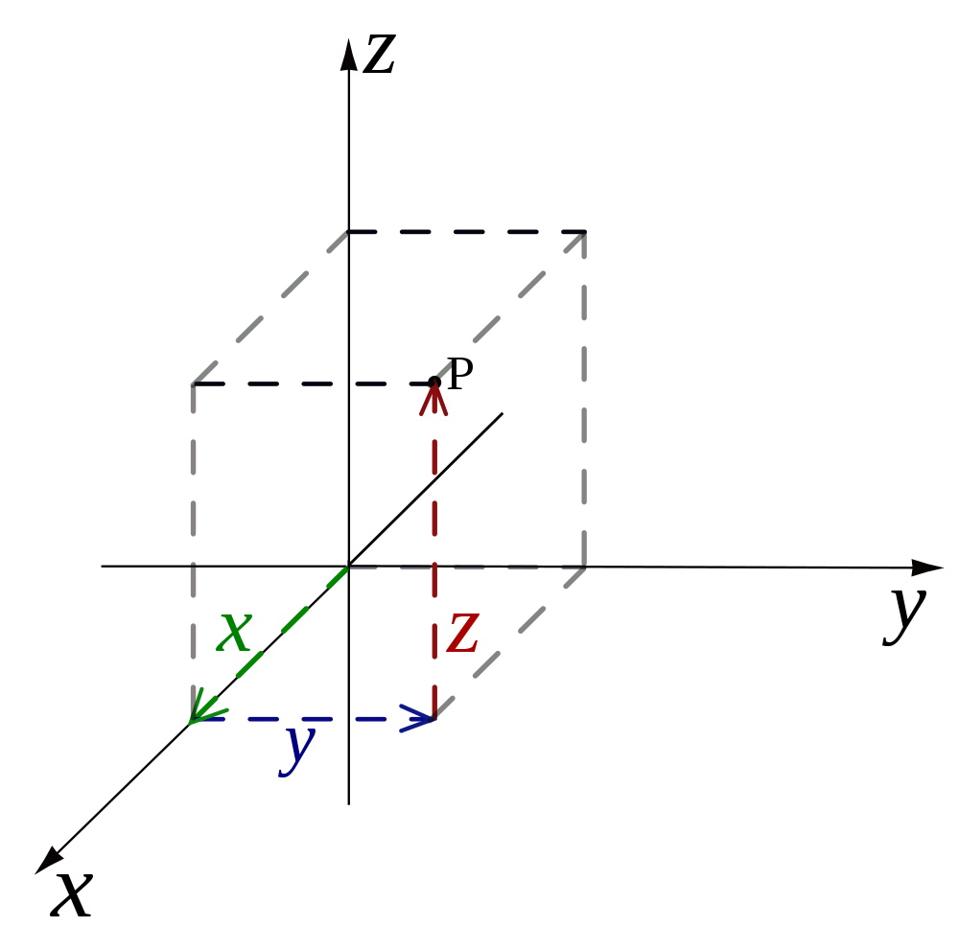
Una delle realizzazioni interessanti e importanti su questa relazione – la distanza tra due punti visualizzata come una linea retta – è che assolutamente non importa come si orienta la visualizzazione delle dimensioni x , y , e z. Puoi:
- modificare le coordinate in modo che le dimensioni x , y , e z siano mutuamente perpendicolari in tutte le direzioni, o
- ruotare questi due punti di qualsiasi quantità in qualsiasi direzione,
e la distanza tra loro non cambierà affatto.
Certo, i singoli componenti cambieranno se ruoti la tua prospettiva o ruoti la linea che collega quei due punti, poiché le tue definizioni di lunghezza, larghezza e profondità cambieranno l’una rispetto all’altra per quella linea mentre si verifica la rotazione.
Ma la distanza complessiva tra questi due punti non cambia affatto; quella quantità di distanza tra quei punti rimane ciò che chiamiamo “invariante” o immutabile, indipendentemente da come vengono ruotati.
Ora, non consideriamo semplicemente lo spazio, ma anche il tempo. Potresti pensare: “beh, se anche il tempo è solo una dimensione, la distanza tra due punti qualsiasi nello spaziotempo funzionerà allo stesso modo“.
Ad esempio, se rappresentiamo la dimensione temporale come t, potresti pensare che la distanza sia la linea retta che collega due punti attraverso le tre dimensioni spaziali oltre alla dimensione temporale. In termini matematici, potresti pensare che l’equazione per la separazione tra due punti qualsiasi sarebbe simile a d = √ ( x ² + y ² + z ² + t ²).
Dopotutto, questo è più o meno lo stesso cambiamento che abbiamo fatto quando siamo passati da due dimensioni a tre dimensioni, tranne che questa volta stiamo passando da tre dimensioni a quattro dimensioni. È un passo ragionevole da tentare e descrive esattamente come sarebbe la realtà se avessimo quattro dimensioni dello spazio, anziché tre.
Ma non abbiamo quattro dimensioni dello spazio; abbiamo tre dimensioni dello spazio e una dimensione del tempo. E nonostante quello che potresti pensare, il tempo non è “solo un’altra dimensione”.

Ci sono due modi in cui il tempo, come dimensione, è diverso dallo spazio.
Connettere spazio e tempo
Il primo modo è facile: non puoi mettere lo spazio (che è una misura della distanza) e il tempo (che è una misura, beh, temporale) sullo stesso piano senza un modo per convertirli l’uno nell’altro.
Fortunatamente, una delle grandi rivelazioni della teoria della relatività di Einstein è che esiste un’importante connessione fondamentale tra distanza e tempo: la velocità della luce, o in maniera equivalente, di qualsiasi particella che viaggia attraverso l’Universo senza una massa a riposo.
La velocità della luce nel vuoto – 299.792.458 metri al secondo – ci dice precisamente come mettere in relazione il nostro movimento nello spazio con il nostro movimento nel tempo: da quella stessa costante fondamentale.
Quando usiamo termini come “un anno luce” o “un secondo luce”, stiamo parlando di distanze in termini di tempo: la quantità di distanza percorsa dalla luce in un anno (o un secondo), per esempio.
Se vogliamo convertire il “tempo” in una distanza, dobbiamo moltiplicarlo per la velocità della luce nel vuoto.
Ma il secondo modo richiede un enorme salto per capirlo: qualcosa che sfuggiva alle più grandi menti della fine del XIX e dell’inizio del XX secolo. L’idea chiave è che ci muoviamo tutti nell’Universo, nello spazio e nel tempo, simultaneamente.
Se stiamo semplicemente seduti qui, fermi e non ci muoviamo affatto nello spazio, allora ci muoviamo nel tempo a una velocità molto specifica che conosciamo tutti: un secondo al secondo.
Tuttavia, e questo è il punto chiave, più velocemente ti muovi nello spazio, più lentamente ti muovi nel tempo.
Le altre dimensioni non si comportano così: il vostro movimento attraverso la x dimensione nello spazio, ad esempio, è completamente indipendente dal movimento attraverso la y e z dimensioni.
Ma il tuo movimento totale nello spazio, e questo è relativo a qualsiasi altro osservatore, determina il tuo movimento nel tempo. Più ti muovi attraverso uno (spazio o tempo), meno ti muovi attraverso l’altro.
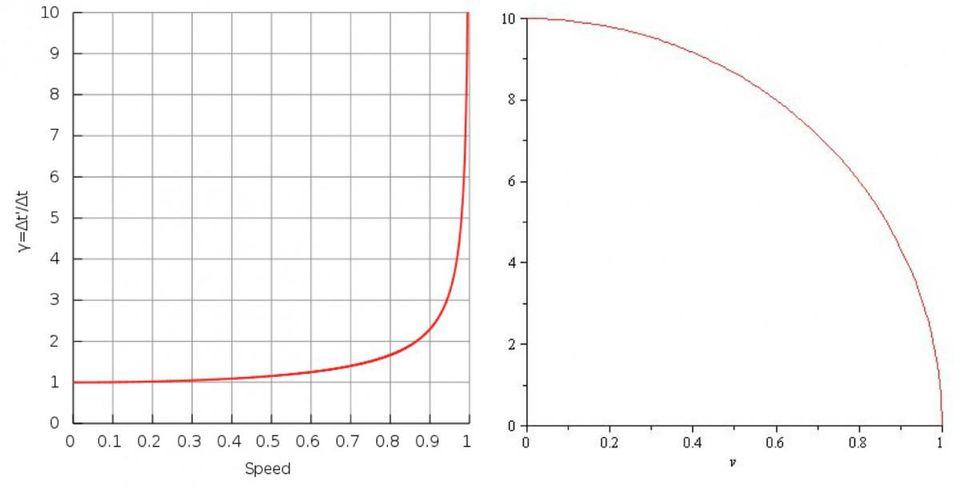
Questo è il motivo per cui la relatività di Einstein ci fornisce concetti come dilatazione del tempo e contrazione della lunghezza.
Se ti muovi a velocità molto basse rispetto alla velocità della luce, non noterai questi effetti: il tempo sembra muoversi a un secondo al secondo per tutti e le lunghezze sembrano essere la stessa distanza per tutti a velocità normalmente raggiungibili sulla Terra.
Ma quando ti avvicini alla velocità della luce, o meglio, quando percepisci un oggetto in cui la velocità relativa tra te ed esso è vicina alla velocità della luce, osserverai che si contrae lungo la sua direzione di movimento relativo e che sembra muoversi a una velocità più lenta (dilatata) rispetto al proprio orologio.
Il motivo alla base di ciò, come realizzato da Einstein, è semplice: succede perché la velocità della luce è la stessa per tutti gli osservatori. Se immagini che un orologio è definito dalla luce che rimbalza avanti e indietro tra due specchi, allora guardare l’orologio di qualcun altro mentre si avvicina alla velocità della luce, inevitabilmente quello che vedrai è che il suo orologio gira più lentamente del tuo.
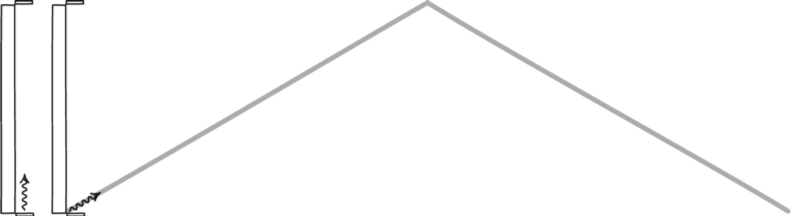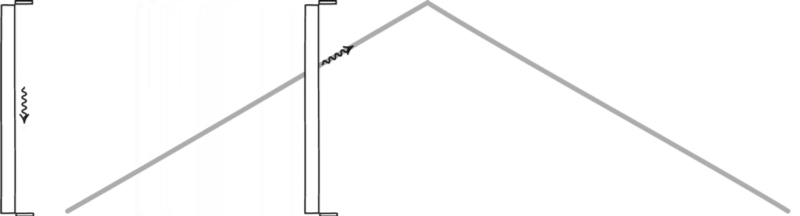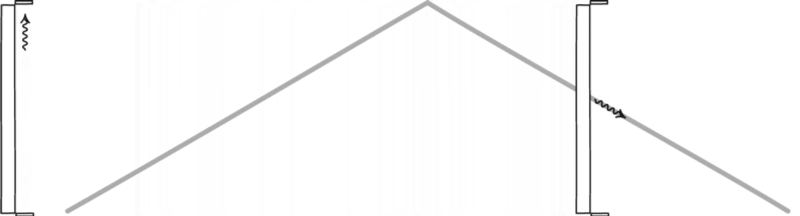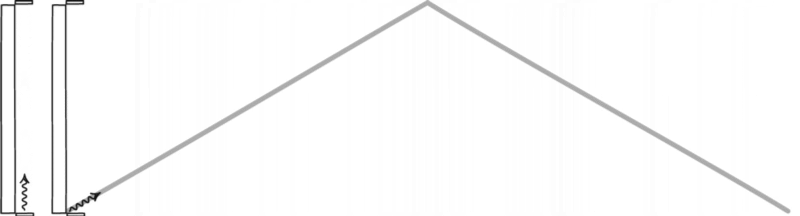
Un orologio luminoso, formato da un fotone che rimbalza tra due specchi, definirà il tempo per qualsiasi osservatore. – JOHN D. NORTON
Ma qui c’è un’intuizione ancora più profonda, che inizialmente sfuggiva persino allo stesso Einstein.
Se tratti il tempo come una dimensione, moltiplicalo per la velocità della luce e – ecco il grande salto – trattalo come se fosse immaginario, piuttosto che reale, allora possiamo definire un “intervallo spaziotemporale” nello stesso modo in cui abbiamo definito la distanza in precedenza.
Solo, poiché il numero immaginario i è solo √ (-1), ciò significa che l’intervallo spaziotemporale è effettivamente d = √ ( x ² + y ² + z ² – c² t ²) [nota il segno meno attaccato alla coordinata temporale!].
In altre parole, la trasformazione da “movimento attraverso o separazione spaziale” a “movimento attraverso o la separazione nel tempo” è anche una rotazione, ma è una rotazione non nelle coordinate cartesiane di spazio (dove x, y, e z sono tutti numeri reali), ma attraverso le coordinate iperboliche dello spaziotempo, dove se le coordinate spaziali sono reali, allora la coordinata temporale deve essere immaginaria.
La persona che per prima mise insieme questi pezzi del puzzle fu l’ex insegnante di Einstein, Hermann Minkowski, che notò nel 1907/8 che,
“D’ora in poi lo spazio da solo, e il tempo da solo, sono destinati a svanire in semplici ombre, e solo una sorta di unione dei due manterrà una realtà indipendente“.
Con il rigore matematico di Minkowski alle spalle, il concetto di spaziotempo non solo è nato, ma è rimasto.
Ciò che è notevole in tutto questo è che Einstein, nonostante non avesse avuto l’intuizione matematica per capire esattamente come la dimensione del tempo fosse correlata alle tre dimensioni convenzionali dello spazio, è stato in grado di mettere insieme questa intuizione fisica chiave.
L’aumento del movimento nello spazio ha ridotto il movimento nel tempo e l’aumento del movimento nel tempo ha ridotto il movimento nello spazio. Tutte le misurazioni dello spazio e del tempo sono significative solo rispetto all’osservatore in questione e dipendono dal movimento relativo dell’osservatore rispetto all’osservato.
Eppure, l’intervallo spaziotemporale rimane invariante. Non importa chi sta osservando o quanto velocemente si sta muovendo, il movimento combinato di qualsiasi oggetto nello spaziotempo è qualcosa su cui tutti gli osservatori possono essere d’accordo.
In un certo senso, il successo della relatività è stato reso ancora più impressionante alla luce della valutazione di Einstein di Minkowski. Parlando al suo studente, Max Born, Minkowski disse quanto segue: “Per me [la relatività] è stata una tremenda sorpresa, perché, quando era studente, Einstein era un vero pigro. Non si è mai preso la briga di impegnarsi in matematica“.
Fortunatamente, in fisica, l’Universo stesso – non l’opinione di nessuno – è l’ultimo arbitro della verità scientifica.
Fonte: Forbes



