Un esperimento apparentemente semplice che prevede misurazioni precise del tempo impiegato da una particella per passare dal punto A al punto B potrebbe innescare una svolta nella fisica quantistica. I risultati potrebbero focalizzare l’attenzione su un’alternativa alla teoria quantistica standard chiamata meccanica Bohmiana, che pone un mondo sotterraneo di onde invisibili che guidano le particelle da un luogo all’altro.
Un nuovo studio, condotto da un team dell’Università Ludwig Maximilian di Monaco (LMU) in Germania, fa previsioni precise per un tale esperimento utilizzando la meccanica bohmiana, una teoria formulata dal fisico teorico David Bohm negli anni ’50 e ampliata dai teorici moderni. La teoria quantistica standard fallisce in questo senso e i fisici devono ricorrere a ipotesi e approssimazioni per calcolare i tempi di transito delle particelle.
“Se le persone sapessero che una teoria che amano così tanto – la meccanica quantistica standard – non può fare previsioni [precise] in un caso così semplice, ciò dovrebbe almeno farle meravigliare“, afferma il teorico e membro del team LMU Serj Aristarchov.
Non è un segreto che il mondo quantistico sia strano. Considera una configurazione che spara elettroni su uno schermo. Non puoi prevedere esattamente dove un dato elettrone atterrerà per formare, diciamo, un punto fluorescente. Ma puoi prevedere con precisione la distribuzione spaziale, o modello, dei punti che prende forma nel tempo man mano che gli elettroni atterrano uno per uno.
Alcune posizioni avranno più elettroni; altri ne avranno di meno. Ma questa stranezza nasconde qualcosa di ancora più strano. A parità di altre condizioni, ogni elettrone raggiungerà il rivelatore in un momento leggermente diverso, il cosiddetto tempo di arrivo. Proprio come le posizioni, i tempi di arrivo avranno una distribuzione: alcuni tempi di arrivo saranno più comuni, altri meno.
Ma la fisica quantistica da manuale non ha un meccanismo per prevedere con precisione questa distribuzione temporale. “La normale teoria dei quanti si occupa solo di ‘dove’; ignorano il ‘quando’”, afferma il membro del team e teorico Siddhant Das. “Questo è un modo per diagnosticare che c’è qualcosa di sospetto“.
C’è una ragione profonda per questa curiosa mancanza. Nella teoria quantistica standard, una proprietà fisica che può essere misurata è chiamata “osservabile“. La posizione di una particella, per esempio, è un osservabile. Ogni osservabile è associato a un’entità matematica corrispondente chiamata “operatore“. Ma la teoria standard non ha un tale operatore per l’osservazione del tempo.
Nel 1933 il fisico teorico austriaco Wolfgang Pauli dimostrò che la teoria quantistica non poteva ospitare un operatore temporale, almeno non nel modo standard in cui la pensiamo. “Concludiamo quindi che l’introduzione di un operatore temporale … deve essere fondamentalmente abbandonato“, ha scritto.
Ma misurare i tempi di arrivo delle particelle e/o il loro “tempo di volo” è un aspetto importante della fisica sperimentale. Ad esempio, tali misurazioni vengono effettuate con rivelatori al Large Hadron Collider o strumenti chiamati spettrometri di massa che utilizzano tali informazioni per calcolare le masse e i momenti di particelle, ioni e molecole.
Anche se tali calcoli riguardano i sistemi quantistici, i fisici non possono utilizzare la meccanica quantistica genuina fino in fondo. “Non avresti modo di fare una previsione [non ambigua]“, dice Das.
Invece ricorrono a ipotesi per arrivare a risposte. Ad esempio, in un metodo, gli sperimentatori presumono che una volta che la particella lascia la sua sorgente, si comporti in modo classico, nel senso che segue le equazioni del moto di Newton.
Ciò si traduce in un approccio ibrido, in parte quantistico e in parte classico. Inizia con la prospettiva quantistica, dove ogni particella è rappresentata da un’astrazione matematica chiamata funzione d’onda. Particelle preparate in modo identico avranno funzioni d’onda identiche quando vengono rilasciate dalla loro sorgente. Ma misurare la quantità di moto di ciascuna particella (o, se è per questo, la sua posizione) all’istante del rilascio produrrà valori diversi ogni volta.
Presi insieme, questi valori seguono una distribuzione che è predetta con precisione dalla funzione d’onda iniziale. Partendo da questo insieme di valori per particelle identicamente preparate, e assumendo che una particella segua una traiettoria classica una volta emessa, il risultato è una distribuzione dei tempi di arrivo al rivelatore che dipende dalla distribuzione del momento iniziale.
La teoria standard viene spesso utilizzata anche per un altro metodo quantomeccanico per il calcolo dei tempi di arrivo. Quando una particella vola verso un rivelatore, la sua funzione d’onda evolve secondo l’equazione di Schrödinger, che descrive il cambiamento di stato di una particella nel tempo. Consideriamo il caso unidimensionale di un rivelatore a una certa distanza orizzontale da una sorgente di emissione.
L’equazione di Schrödinger determina la funzione d’onda della particella e quindi la probabilità di rilevare quella particella in quella posizione, assumendo che la particella attraversi la posizione solo una volta (non esiste, ovviamente, un modo chiaro per convalidare questa ipotesi nella meccanica quantistica standard). Utilizzando tali ipotesi, i fisici possono calcolare la probabilità che la particella arrivi al rivelatore in un dato momento ( t ) o prima.
“Dal punto di vista della meccanica quantistica standard, suona perfettamente bene“, afferma Aristarhov. “E ti aspetti di avere una bella risposta da questo“.
C’è un intoppo, tuttavia. Passare dalla probabilità che il tempo di arrivo sia minore o uguale a t alla probabilità che sia esattamente uguale a t implica il calcolo di una quantità che i fisici chiamano flusso quantistico, o corrente di probabilità quantistica, una misura di come la probabilità di trovare la particella nella posizione del rivelatore cambia con il tempo.
Funziona bene, tranne per il fatto che, a volte, il flusso quantistico può essere negativo anche se è difficile trovare funzioni d’onda per le quali la quantità diventa sensibilmente negativa. Ma nulla “proibisce che questa quantità sia negativa“, dice Aristarhov. “E questo è un disastro“. Un flusso quantistico negativo porta a probabilità negative e le probabilità non possono mai essere inferiori a zero.
L’utilizzo dell’equazione di Schrödinger per calcolare la distribuzione dei tempi di arrivo funziona solo quando il flusso quantistico è positivo, un caso che, nel mondo reale, esiste definitivamente solo quando il rivelatore si trova nel “campo lontano” o a una distanza considerevole dal sorgente e la particella si muove liberamente in assenza di potenziali.
Quando gli sperimentali misurano tempi di arrivo così lontani, sia l’approccio ibrido che quello del flusso quantistico fanno previsioni simili che combaciano bene con i risultati sperimentali. Ma non fanno previsioni chiare per i casi “near field“, in cui il rivelatore è molto vicino alla sorgente.
Previsioni Bohmiane
Insoddisfatti di questo status quo imperfetto, nel 2018 Das e Aristarhov, insieme al loro allora Ph.D. il consulente Detlef Dürr, un esperto di meccanica bohmiana presso LMU, deceduto all’inizio di quest’anno, e i loro colleghi, hanno iniziato a lavorare sulle previsioni dei tempi di arrivo basate sulla Bohm.
La teoria di Bohm sostiene che ogni particella è guidata dalla sua funzione d’onda. A differenza della meccanica quantistica standard, in cui si ritiene che una particella non abbia una posizione o un momento precisi prima di una misurazione, e quindi nessuna traiettoria, le particelle nella meccanica bohmiana sono reali e hanno traiettorie ondulate descritte da precise equazioni del moto (anche se diverse dalle equazioni del moto di Newton).
Tra le prime scoperte dei ricercatori c’era che le misurazioni del campo lontano non sarebbero riuscite a distinguere tra le previsioni della meccanica bohmiana e quelle degli approcci ibridi o di flusso quantistico. Questo perché, su grandi distanze, le traiettorie Bohmiane diventano linee rette, quindi vale l’approssimazione semi-classica ibrida.
Inoltre, per traiettorie rettilinee in campo lontano, il flusso quantistico è sempre positivo e il suo valore è previsto esattamente dalla meccanica bohmiana. “Se metti un rivelatore abbastanza lontano, e fai l’analisi Bohmiana, vedi che coincide con l’approccio ibrido e l’approccio del flusso quantistico“, dice Aristrhov.
La chiave, quindi, è eseguire misurazioni in campo vicino, ma queste sono state considerate impossibili. “Il regime del campo vicino è molto volatile. È molto sensibile alla forma della funzione d’onda iniziale che hai creato”, afferma Das. Inoltre, “se ti avvicini molto alla regione della preparazione iniziale, la particella verrà rilevata istantaneamente. Non puoi risolvere [i tempi di arrivo] e vedere le differenze tra questa previsione e quella previsione“.
Per evitare questo problema, Das e Dürr hanno proposto una configurazione sperimentale che consentisse di rilevare le particelle lontano dalla sorgente, generando comunque risultati unici che potessero distinguere le previsioni della meccanica bohmiana da quelle dei metodi più standard.
Concettualmente, la configurazione proposta dal team è piuttosto semplice. Immagina una guida d’onda, un percorso cilindrico che confina il movimento di una particella (una fibra ottica è una tale guida d’onda per i fotoni di luce, per esempio).
Su un’estremità della guida d’onda, prepara una particella, idealmente un elettrone o una particella di materia, nella sua energia più bassa, o terra, e intrappolala in un pozzo di potenziale elettrico a forma di ciotola. Questo pozzo è in realtà il composto di due potenziali barriere adiacenti che creano collettivamente la forma parabolica. Se una delle barriere viene spenta, la particella sarà ancora bloccata dall’altra che rimane in posizione, ma è libera di fuoriuscire dal pozzo nella guida d’onda.
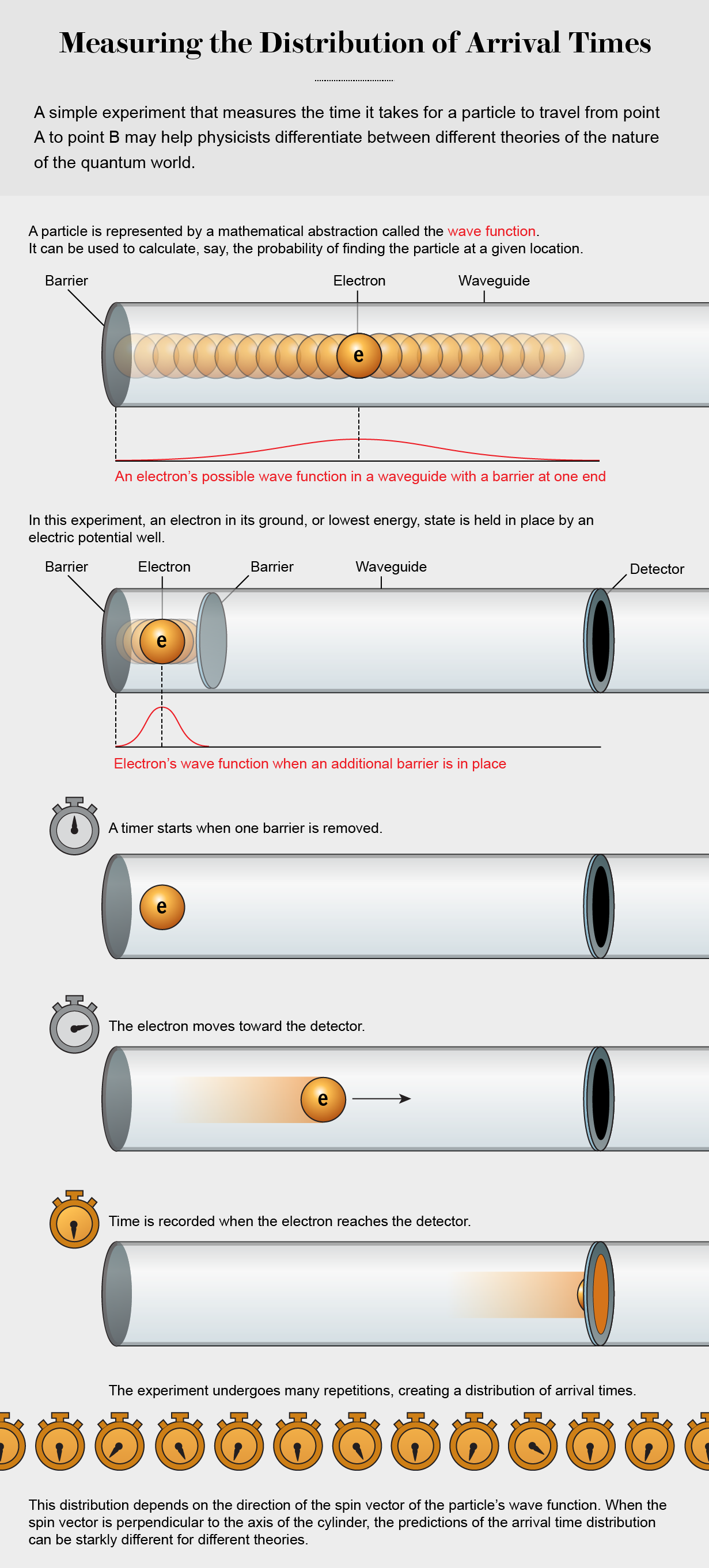
Das ha svolto il compito meticoloso di arricchire i parametri dell’esperimento, eseguendo calcoli e simulazioni per determinare la distribuzione teorica dei tempi di arrivo a un rivelatore posizionato lontano da una sorgente lungo l’asse di una guida d’onda. Dopo alcuni anni di lavoro, aveva ottenuto risultati chiari per due diversi tipi di funzioni d’onda iniziali associate a particelle come gli elettroni. Ogni funzione d’onda può essere caratterizzata da qualcosa chiamato vettore di spin.
Immagina una freccia associata alla funzione d’onda che può puntare in qualsiasi direzione. Il team ha esaminato due casi: uno in cui la freccia punta lungo l’asse della guida d’onda e un altro in cui è perpendicolare a tale asse.
Il team ha dimostrato che, quando il vettore di spin della funzione d’onda è allineato lungo l’asse della guida d’onda, la distribuzione dei tempi di arrivo previsti dal metodo del flusso quantistico e dalla meccanica bohmiana sono identiche. Ma differiscono significativamente dall’approccio ibrido.
Quando il vettore di spin è perpendicolare, tuttavia, le distinzioni diventano più nette. Con l’aiuto del loro collega della LMU Markus Nöth, i ricercatori hanno dimostrato che tutte le traiettorie bohmiane colpiranno il rivelatore in corrispondenza o prima di questo tempo limite. “Questo è stato molto inaspettato“, dice Das.
Ancora una volta, la previsione Bohmiana differisce significativamente dalle previsioni della teoria ibrida semi-classica, che non mostrano un taglio così netto del tempo di arrivo. E soprattutto, in questo scenario, il flusso quantistico è negativo, il che significa che il calcolo dei tempi di arrivo utilizzando l’equazione di Schrödinger diventa impossibile. I teorici quantistici standard “alzano le mani quando [il flusso quantistico] diventa negativo“, dice Das.
Ma la meccanica bohmiana continua a fare previsioni. “C’è una chiara distinzione tra [questo] e tutto il resto“, dice Aristarhov.
Il teorico quantistico Charis Anastopoulos dell’Università di Patrasso in Grecia, un esperto di tempi di arrivo, che non è stato coinvolto in questo lavoro, è sia impressionato che circospetto. “La configurazione che stanno proponendo sembra plausibile“, dice. E poiché ogni approccio al calcolo della distribuzione dei tempi di arrivo implica un modo diverso di pensare alla realtà quantistica, una chiara scoperta sperimentale potrebbe scuotere le basi della meccanica quantistica.
“Rivendicherà particolari modi di pensare. Quindi, in questo modo, avrà un certo impatto“, afferma Anastopoulos. “Se [è d’accordo con] la meccanica bohmiana, che è una previsione molto particolare, questo sarebbe un grande impatto, ovviamente“.
Almeno uno sperimentatore si sta preparando per realizzare la proposta del team. Prima della morte di Dürr, Ferdinand Schmidt-Kaler dell’Università Johannes Gutenberg di Magonza in Germania aveva discusso con lui sui tempi di arrivo. Schmidt-Kaler è un esperto di un tipo di trappola ionica in cui i campi elettrici vengono utilizzati per confinare un singolo ione calcio. Una serie di laser viene utilizzata per raffreddare lo ione al suo stato fondamentale quantistico, dove l’impulso e le incertezze di posizione dello ione sono al minimo.
La trappola è una regione tridimensionale a forma di ciotola creata dalla combinazione di due potenziali elettrici; lo ione si trova alla base di questo potenziale “armonico“. La disattivazione di uno dei potenziali crea condizioni simili a quanto richiesto dalla proposta teorica: una barriera da un lato e un potenziale elettrico inclinato dall’altro. Lo ione si muove lungo quel pendio, accelera e guadagna velocità. “Puoi avere un rilevatore fuori dalla trappola e misurare l’orario di arrivo“, afferma Schmidt-Kaler. “Questo è ciò che lo ha reso così attraente“.
Per ora, il suo gruppo ha condotto esperimenti in cui i ricercatori espellono lo ione dalla sua trappola e lo rilevano all’esterno. Hanno dimostrato che il tempo di volo dipende dalla funzione d’onda iniziale di una particella. I risultati sono stati pubblicati quest’anno sul New Journal of Physics. Schmidt-Kaler e i suoi colleghi hanno anche eseguito test non ancora pubblicati dello ione che esce dalla trappola solo per essere riflesso da uno “specchio elettrico” e ripreso, un processo che l’installazione ottiene con un’efficienza del 98%, afferma. “Siamo in corso“, afferma Schmidt-Kaler. “Naturalmente, non è sintonizzato per ottimizzare questa misurazione del tempo di distribuzione del volo, ma potrebbe esserlo“.
È più facile a dirsi che a farsi. Il rivelatore al di fuori della trappola ionica sarà probabilmente un foglio di luce laser e il team dovrà misurare l’interazione dello ione con il foglio di luce con una precisione di nanosecondi. Gli sperimentatori dovranno anche disattivare metà del potenziale armonico con una precisione temporale simile, un’altra seria sfida. Queste e altre insidie abbondano nel tortuoso sentiero che deve essere percorso tra previsione teorica e realizzazione sperimentale.
Tuttavia, Schmidt-Kaler è entusiasta delle prospettive di utilizzare le misurazioni del tempo di volo per testare le basi della meccanica quantistica. “Questo ha l’attrazione di essere completamente diverso da altri [tipi di] test. È davvero qualcosa di nuovo“, dice. “Questo passerà attraverso molte iterazioni. Vedremo i primi risultati, spero, nel prossimo anno. Questa è la mia chiara aspettativa“.
Nel frattempo, Aristarhov e Das si stanno rivolgendo anche ad altri. “Speriamo davvero che gli sperimentalisti di tutto il mondo notino il nostro lavoro”, afferma Aristarhov. “Uniremo le forze per fare gli esperimenti“.
E una conclusione scritta da Dürr in un articolo ancora da pubblicare contiene parole finali che potrebbero quasi essere un epitaffio: “Dovrebbe essere chiaro ormai che il capitolo sulle misurazioni del tempo nella fisica quantistica può essere scritto solo se il vero tempo di meccanica quantistica, i dati di volo, diventano disponibili“, ha scritto.
Quale teoria verrà considerata corretta dai dati sperimentali, se presente? “È una domanda molto eccitante“, ha aggiunto Dürr.
