La cosmologia è lo studio dell’Universo: dalle scale più piccole alle più grandi. Se vogliamo capire questo Universo in cui abitiamo, non abbiamo altra scelta che considerare tutto insieme, dalle particelle subatomiche che compongono la nostra realtà alle strutture su più ampia scala che formano. Ciò richiede la comprensione non solo dei vari quanti che si legano e compongono tutto ciò che possiamo osservare e con cui possiamo interagire, ma anche lo stadio su cui si muovono. L’Universo non esiste semplicemente, ma si evolve sia con lo spazio che con il tempo mentre la nostra storia cosmica si svolge.
Fu appena un secolo fa, nel 1915, che Einstein svelò per la prima volta la teoria della relatività generale, che descriveva in dettaglio come lo spazio e il tempo influenzano la materia e l’energia al suo interno e come, al contrario, la materia e l’energia al suo interno determinano forma ed evoluzione dello spaziotempo. Sorprendentemente, fu solo sette anni dopo, ben 100 anni fa, che l’equazione più importante in cosmologia è stata derivata per la prima volta: la prima equazione di Friedmann.
A un non esperto, potrebbe sembrare uno scherzo che l’equazione di Friedmann, e non la legge di Hubble, sia elevata a una posizione così stimata. Ma per qualsiasi esperto, è l’unica scelta che vale la pena considerare. Ecco perché.
Quando si tratta delle regole che governano il tessuto stesso dell’Universo, la Relatività Generale di Einstein è l’unico gioco in città. Se puoi scrivere come, in qualsiasi momento, viene distribuita la materia e l’energia nell’Universo, le equazioni di Einstein ti diranno come il tessuto dello spaziotempo è curvo in ogni punto del cosmo. Al contrario, la curvatura dello spaziotempo, se la conoscete, dirà a ogni quanto di materia ed energia come muoversi all’interno di quell’Universo. È una danza complessa, ma le equazioni di campo di Einstein sono abbastanza complete da fornirci queste informazioni per qualsiasi distribuzione di materia che possiamo immaginare.
Naturalmente, questo sistema di 16 equazioni accoppiate – 10 delle quali sono indipendenti l’una dall’altra – diventa sempre più difficile da scrivere, per non parlare di risolvere, tanto più complicata è la distribuzione di materia ed energia. Se facciamo ipotesi semplificative, tuttavia, a volte possiamo trovare soluzioni esatte per questi casi idealizzati.
In tutte le direzioni, ovunque guardiamo, vediamo che l’Universo è più o meno lo stesso: ci sono stelle e galassie ovunque, più o meno nello stesso numero, in tutte le località e regioni dello spazio. Se immagini che l’Universo nel suo insieme abbia queste proprietà — cioè è isotropo (lo stesso in tutte le direzioni) e omogeneo (lo stesso in tutti i luoghi) — puoi descrivere lo spaziotempo globale molto semplicemente. La struttura dello spaziotempo porta quindi direttamente a un insieme di equazioni che predicono come si evolverà l’Universo: quelle sono le equazioni di Friedmann.
Molto semplicemente, la prima di queste equazioni contiene solo quattro termini importanti, ognuno dei quali ha qualcosa di importante da dire su un Universo che è, almeno nella media cosmica su larga scala, lo stesso ovunque e in tutte le direzioni.
- Sul lato sinistro c’è un termine che rappresenta il cambiamento nella scala dell’Universo diviso per la scala dell’Universo; questa è la definizione del parametro Hubble, che governa il modo in cui l’Universo si espande o si contrae nel tempo.
- Sul lato destro, il primo termine rappresenta tutta la materia e l’energia che si trova nell’Universo in tutte le sue varie forme: materia normale, materia oscura, radiazione, neutrini, ecc.
- Il secondo termine sul lato destro rappresenta la curvatura globale dello spaziotempo e determina se l’Universo è aperto, chiuso o spazialmente piatto.
- E il terzo e ultimo termine sul lato destro è la costante cosmologica di Einstein, che determina l’energia che non può essere districata dallo spazio stesso.
La cosa forse più notevole di questa equazione, tuttavia, sono le sue implicazioni. Se hai un Universo pieno, uniformemente, di qualsiasi tipo di materia ed energia, indipendentemente dalla curvatura o dal valore della costante cosmologica, allora il tuo Universo non può essere statico. Deve espandersi o contrarsi, e cosa sta accadendo è qualcosa che puoi sapere solo misurando l’Universo.
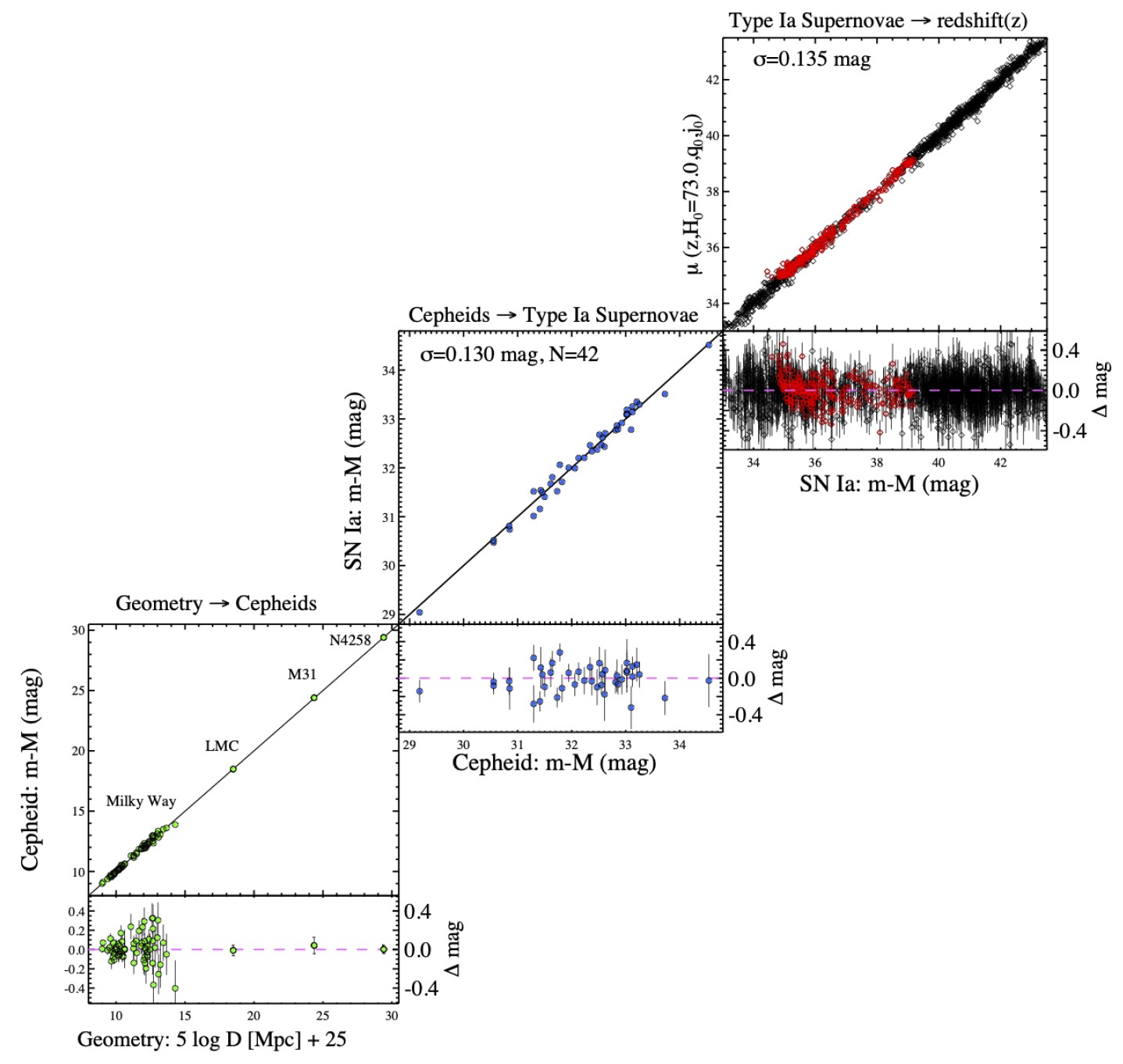
Quindi diciamo che lo fai: esci e misuri l’Universo. Si misura il tasso di espansione o contrazione in questo momento, nonché come (o se) è cambiato nel tempo. Decidi tu quali sono i vari tipi di materia ed energia e quanta ce n’è di ogni tipo. Si misura la quantità di curvatura spaziale o si scopre che l’Universo è piatto fino ai limiti delle proprie capacità di misurazione. E si misura anche la costante cosmologica, che si comporta in modo identico a una forma di energia la cui densità di energia rimane costante, indipendentemente da come la scala dell’Universo si evolve nel tempo.
Cos’altro ti dà questa equazione di Friedmann?
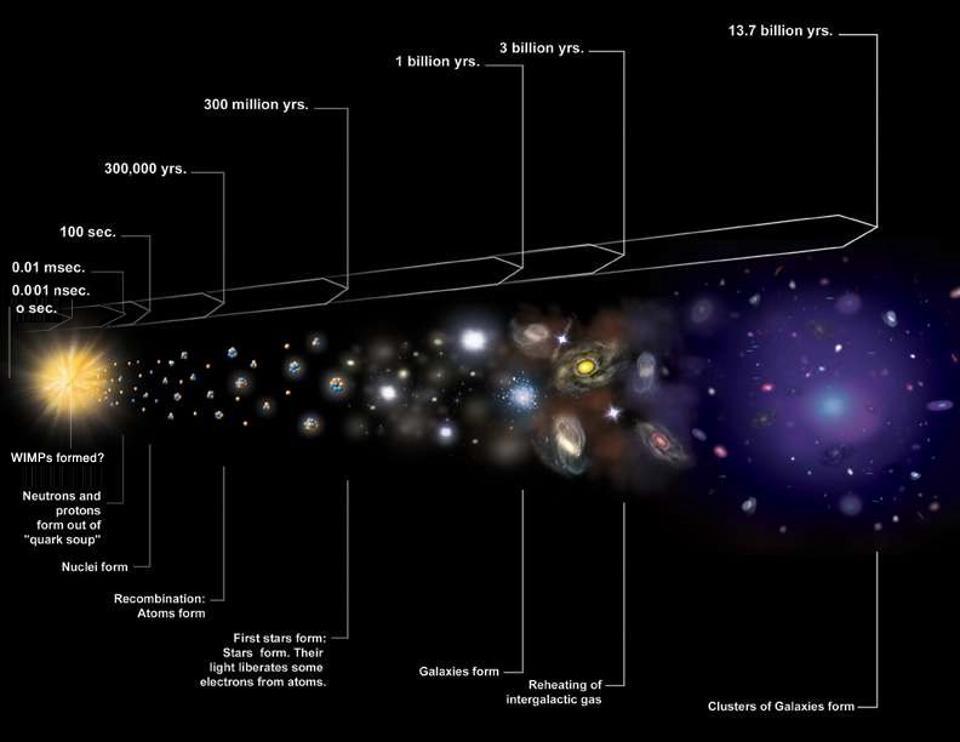
L’intera storia dell’Universo, sia passata che futura. Ti permette di dedurre, se l’Universo si sta espandendo, quanto fossero calde e dense le cose in qualsiasi momento nel passato dell’Universo. Se hai radiazioni, ti consente di dedurre quando:
- è diventato troppo caldo per formare atomi neutri,
- è diventato troppo caldo per formare nuclei atomici,
- è diventato troppo caldo per avere protoni e neutroni individuali,
- l’Universo ha creato spontaneamente coppie materia/antimateria,
e anche per concludere che l’Universo è partito da uno stato caldo, denso, in rapida espansione: quello che oggi chiamiamo il caldo Big Bang.
La prima equazione di Friedmann consente anche di quantificare quanto significativamente la luce di un oggetto distante sarà spostata verso il rosso (o verso il blu) in un Universo in espansione (o contrazione). Se conosci la velocità di espansione (o contrazione) e le proprietà quantomeccaniche intrinseche degli atomi, allora puoi uscire e misurare un oggetto distante e calcolare quanto gravemente la luce sarà influenzata dall’evoluzione dello spaziotempo all’interno dell’Universo.
Questo è ciò che chiamiamo legge di Hubble. In altre parole, sebbene la legge di Hubble sia stata derivata empiricamente – cioè sia stata determinata dalle sole osservazioni, indipendentemente dalla teoria sottostante – può essere derivata teoricamente esclusivamente da questa importantissima equazione.
Sebbene sia stato Hubble a misurare per primo le distanze delle galassie al di fuori della Via Lattea, è stato un astrofisico molto meno noto, Georges Lemaître, che per primo ha messo insieme tutti i pezzi sulle nostre origini cosmiche. Lavorando nell’ambito delle equazioni di Friedmann ed estraendo i primi dati sulla distanza pubblicati da Hubble, il suo associato Humason, insieme ai dati di spostamento verso il rosso dalle precedenti osservazioni fatte da Vesto Slipher, Lemaître:
- derivò la legge di Hubble,
- fece la prima stima del tasso di espansione dell’Universo,
- e avanzò la sorprendente conclusione che l’Universo non è eterno, ma piuttosto iniziò un periodo limitato di tempo fa con un caldo Big Bang.
Era il 1927, e dopo aver inviato una lettera sulle sue conclusioni a Einstein, che gli aveva inviato una risposta leggendariamente sprezzante (e scorretta) in cui diceva che la sua “la matematica era corretta, ma la [sua] fisica era abominevole“, sarebbe toccato a Howard Robertson (nel 1928) e infine, con grande clamore, allo stesso Hubble nel 1929, di portare l’idea dell’Universo in espansione nel mainstream.
In modo simile, la prima equazione di Friedmann può essere utilizzata anche per far evolvere l’Universo in avanti nel tempo. Devi capire che il tipo di equazione più potente in tutta la fisica è un’equazione differenziale, ed è esattamente ciò che è la prima equazione di Friedmann.
Perché le equazioni differenziali sono così importanti?
Perché questi sono i tipi di equazioni che ti consentono, se sai come si comporta un sistema fisico in un determinato momento, di far evolvere il tuo sistema in avanti o indietro nel tempo: al momento successivo o al momento precedente. Ma il vero potere di un’equazione differenziale può essere visto quando arrivi a quel momento successivo o precedente, perché è proprio quella stessa equazione, solo con i nuovi valori per le proprietà fisiche del sistema in quel momento, che ti dirà di nuovo cosa accade nel momento successivo o precedente.
La prima equazione di Friedmann, quindi, ti consente sia di tracciare la storia dell’Universo indietro nel tempo finché si applica quell’equazione, sia anche avanti nel tempo allo stesso modo. Supponendo che non ci siano cambiamenti bruschi e colossali nei tipi di energia che compongono l’Universo, misurare l’Universo come è oggi ci permette di concludere quale sarà il suo destino finale.
Eppure, nonostante tutto ciò, la prima equazione di Friedmann non è stata completata. In media – sulla più grande delle scale cosmiche – l’Universo è davvero isotropo e omogeneo. Se dovessi disegnare una sfera, diciamo, di circa 10 miliardi di anni luce di diametro, attorno a qualsiasi regione del nostro Universo osservabile, racchiuderesti solo lo 0,1% circa del volume dell’Universo visibile. Eppure, sia che tu abbia disegnato quella sfera attorno all’ammasso di galassie più denso del cosmo o al più rado vuoto cosmico, se avessi sommato tutta la materia e l’energia all’interno di quella sfera, otterresti lo stesso valore preciso con una precisione di circa il 99,99%. L’Universo, su scale più grandi, è uniforme a ben 1 parte su 30.000.
Ma se scendi a piccole scale cosmiche, a cose come ammassi di galassie, gruppi galattici, singole galassie, o anche più piccoli a ammassi stellari, singoli sistemi stellari o anche a stelle e/o pianeti isolati, scoprirai che l’Universo è notevolmente disuniforme.
Indovina un po?
La prima equazione di Friedmann permette di derivarla. Ti permette di derivare e quantificare il livello di non uniformità – l’allontanamento dall’isotropia e dall’omogeneità – su qualsiasi scala cosmica in qualsiasi momento. Aggiungendo perturbazioni disomogenee (cioè non uniformi) in cima allo sfondo altrimenti uniforme, possiamo derivare la presenza e la crescita della struttura cosmica.
Ci sono un certo numero di persone che, nel passato, temevano che l’ipotesi di uniformità nell’Universo non fosse buona. Ci sono ancora un gruppo di fisici, anche se pochissimi astrofisici che lavorano sia sul lato teorico che sull’osservazione, che temono che l’Universo possa essere troppo disomogeneo perché la prima equazione di Friedmann possa essere applicata al nostro Universo così com’è.
Il fatto è che, se sei preoccupato per questo, ci sono domande che dovresti legittimamente porre.
- Esiste un quadro di riferimento preferito?
- Le galassie ruotano in senso orario più frequentemente di quanto non ruotino in senso antiorario?
- Ci sono prove che i quasar esistano solo a multipli di uno specifico spostamento verso il rosso?
- La radiazione cosmica di fondo a microonde devia da uno spettro di corpo nero?
- Ci sono strutture troppo grandi per essere spiegate in un universo mediamente uniforme?
Anche se la maggior parte di coloro che mettono in dubbio l’omogeneità dell’Universo si rifiutano di ammetterlo, la verità è che controlliamo e testiamo questi presupposti tutto il tempo. Per farla breve, nonostante l’occasionale affermazione che persista una grande disomogeneità, non ce n’è nessuno che abbia mai resistito al controllo.
L’unico quadro di riferimento degno di nota è quello in cui il bagliore residuo del Big Bang appare uniforme nella temperatura. È probabile che le galassie siano “mancine” come “destre”. Gli spostamenti verso il rosso di Quasar non sono definitivamente quantizzati. La radiazione del fondo cosmico a microonde è il corpo nero più perfetto che abbiamo mai misurato. Ed è probabile che i grandi gruppi di quasar che abbiamo scoperto siano solo pseudo-strutture e non legati gravitazionalmente insieme in alcun senso significativo.
Se la prima equazione di Friedmann è valida, allora non solo possiamo determinare sia l’origine che il destino del nostro Universo, ma possiamo derivare tutti i tipi di proprietà sull’Universo in qualsiasi momento.
- Possiamo determinare quale fosse e sarà l’importanza relativa di tutte le diverse forme di materia ed energia in qualsiasi momento della storia cosmica.
- Possiamo determinare la densità assoluta di ogni componente dell’Universo in qualsiasi momento della nostra storia cosmica.
- Possiamo determinare sia il tasso di espansione che la variazione del tasso di espansione nel tempo in qualsiasi momento della storia cosmica.
- Possiamo determinare tutte le diverse “epoche” che il nostro Universo ha attraversato, incluso quando era dominato dalle radiazioni, dalla materia oscura e dall’energia oscura.
E se ci fossero state altre componenti dell’Universo che hanno dominato, come i neutrini, la materia normale, le stringhe cosmiche o qualcosa di ancora più esotico, saremmo in grado di determinare anche questo. Dal punto di vista osservativo, possiamo ricavare quanto grande sembrerebbe un oggetto o quanto luminoso sembrerebbe in base a quanto era lontano quando emetteva la sua luce all’interno dell’Universo in espansione. Praticamente qualsiasi proprietà che vorresti sapere – spostamento verso il rosso, distanza, tasso di espansione, tempo di ricerca, ecc. – può essere derivata da poco più di questa equazione, da sola.
Naturalmente, ci sono dei limiti a ciò che la prima equazione di Friedmann può fare. Non può descrivere in modo fluido cosa succede in regioni dello spazio che non si espandono più, come strutture legate gravitazionalmente come galassie e gruppi di galassie. Inoltre, non può descrivere in modo fluido cosa è successo quando si sono verificate brusche transizioni nei contenuti energetici dell’Universo, come alla fine dell’inflazione e all’inizio del caldo Big Bang. Ma dai primi momenti in cui il caldo Big Bang si applica a tutto il futuro che crediamo di poter estrapolare, la prima equazione di Friedmann è davvero l’equazione più importante di tutto l’Universo.
Le equazioni di Friedmann, e in particolare la prima equazione di Friedmann – che mette in relazione il tasso di espansione dell’Universo con la somma totale di tutte le diverse forme di materia ed energia al suo interno – sono note da 100 anni interi, mentre gli esseri umani si sono applicati all’Universo per quasi lo stesso tempo. Ci ha mostrato come l’Universo si è espanso nel corso della sua storia e ci consente di prevedere quale sarà il nostro destino cosmico finale, anche in un futuro ultra lontano.
Ma possiamo solo essere certi che le nostre conclusioni siano corrette a un particolare livello di confidenza; se c’è un cambiamento improvviso nei contenuti dell’Universo, le conclusioni che abbiamo tratto sul nostro futuro non sono più certe. Al di là dei limiti dei nostri dati, dobbiamo sempre rimanere scettici nel trarre anche le conclusioni più convincenti. Al di là del noto, le nostre migliori previsioni possono rimanere solo mere speculazioni.
